Published on October 17th 2023 | 5 mins , 917 words
KCSE Mathematics Paper 1 Revision
Prepare for Kenya Certificate of Secondary Education Maths Paper 1 here !
An aircraft company bought eight aircrafts for eighteen billion, nine hundred and seventy-five million, twenty-eight thousand, two hundred and fourty
(a) Write the total cost of the eight aircrafts in figures
18,975, 028,240
(b) Calculate the cost of each aircraft
\(\frac{18,975, 028,24} {8}\)
\(2,371,878,530\)
2. Solve for x in the equation
\(\frac{3}{x+1}+ \frac{2}{x+5}= \frac{1}{x-2} \)
\(\frac{3x+15+2x+2}{(x+1)(x+5)}= \frac{1}{x-2} \)
\((x-2)(5x+17)\)
\(=(x+1)(x+5)\)
\(5x^{2}+17x-10x+34\)
\(=x^{2}+6x+5\)
\(4x^{2}+x-39=0\)
\(x=\frac{-1\pm\sqrt{1-16\times39}}{8}\)
\(x=3 \: or \: x=-3.25\)
3a) The number 16200 is given as \(2^{x}\times 3^{y}\times5^{z}\)
Find the value of \(x+y+z\)
\(16200= 2^{3}\times 3^{4}\times5^{2}\)
x=3,y=4 and z=2
x+y+z=3+4+2=9
b) When a number N is multiplied by 16200, a perfect cube is obtained. Find the least value of N
\(2^{3}\times 3^{4}\times5^{2}\)
$$2^{0}\times 3^{2}\times5^{1}$$
\(=45\)
4. Given that \(\sin\alpha^{\circ}=\frac{1}{\sqrt{5}}\) where \(\alpha \) is an acute angle, find without using mathematical tables
(a) \(cos \alpha^{\circ} \) in the form of \(a\sqrt{b}\) where \(a\) and \(b\) are rational numbers

\(=\frac{2\sqrt{5}}{\sqrt{5}\sqrt{5}}\)
\(=\frac{2\sqrt{5}}{5}\)
(b) \(\tan (90-\alpha)^{\circ}\)
\(=\frac{2}{1}=2\)
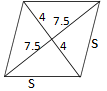
5. The area of a rhombus is \(60cm^{2}\). If the shorter diagonal is 8 cm. Find the perimeter of the rhombus (4mks)
Area = \(\frac{1}{2}\times D \times d\)
60 = \(\frac{1}{2}\times D \times 8\)
\(\Rightarrow 4D=60\)
D = 15 cm
\(s^{2}= 7.5^{2} + 4^{2}\)
\(s^{2}=72.25 \)
\(s = 8.5 cm\)
P = 4s
P = \(4 \times 8.5 \)
P = 34 cm
6. A 63 kg metal of density, 7000 \(kg/m^{3}\) is moulded into a rectangular pipe with external dimensions of 12 cm by 15 cm and internal dimensions of 10 cm by 12 cm. Calculate the length of the pipe in metres.
Volume of material used to make the pipe \(V_{1}\) = \(\frac{mass}{densiry}\)
\(V_{1}\) = \(\frac{63}{7000}\)
= 0.009 \(m^{3}\)
= \(0.009 \times 1000000 \: cm^{3}\)
= \(9000 \: cm^{3} \)
Cross-sectional area of the rectangular pipe
= \((12 \times 15)\) - \((10 \times 12)\)
= \( 60 \: cm^{2}\)
But Volume equals cross-sectional area \(\times\) length
This implies that length of the pipe therefore = \(\frac{volume}{cross-sectinal \: area}\)
= \(\frac{9000}{60}\)
= 150 cm
= 1.5 m
3. The interior angle of a regular polygon is 300 more than four times the exterior angle. Find the number of sides of the polygon. (3 marks)
4. A company sales lady sold goods worth Ksh. 360,000 but gave a discount of 2.5%, if she is paid a commission of 8% on her sales and her basic salary of Ksh. 12,000, calculate her earnings in that month. (3 marks)
5. Given the curve y = \(x^3 + 2x^2 – 6x + 1\). Find the equation of the normal to the curve at x = 1. (3 marks)
10. A bus takes 40 minutes, 45 minutes and 48 minutes to travel from town P to town S via towns Q and R respectively. If the bus is to arrive in town S on Tuesday 1.13 a.m., find the time it should depart from town P. (3 marks)
11. A well wisher distributed his computers as follows: A certain hospital received a quarter of the total number of computers, a nearby school received a half of the remainder and a self help group received a third of what the school received. What remained were six computers more that the self help group received. How many computers did the well wisher have? (4 marks)
12. Draw a line AB 12cm long. Using ruler, set square and compasses only, construct the point X which divides the line AB internally in the ratio 5:3. measure AX. (3 marks)
13. Using mid-ordinate rule with four strips, estimate the area bounded by the curve \(y = 2^x + 3x^2\), the x – axis, the lines x = 0 and x = 2. (3 marks)
14. If Tan A = ¾, show that Cos2 A + Sin 2 A = 1 (3 marks)
SECTION II (50 MARKS)
Answer ONLY 5 Questions in this Section
17. Water flows through a pipe of internal radius of 3.5cm at 9 metres per second into a storage tank of rectangular base of 12m by 8m.
Calculate
a) The volume of water delivered into the tank in one minute in litres. (2 marks)
b) The capacity of water in litres that is consumed by a village of 435 families that depend on this water, in one week, if each family consumes an average of six jericans of 20 litres each per day. (2 marks)
c) The minimum height of the water level in the storage tank that will ensure that the village doesn’t suffer from water shortage within the week. (2 marks)
d) How long will it take the pipe to fill the tank to that level giving your answer in hours. (2 marks)
e) Calculate the monthly bill of the village if the cost of water is Kshs.1.50 per jelican (take a month of 30 days) (2 marks)
18. A marble is projected up and after t seconds its distance from the starting point is S metres
where S = 24t – 3t2.
(i) Find the distance covered after 8 seconds. (2 marks)
(ii) What is the velocity after 8 seconds? (2 marks)
(iii) What is its initial velocity? (2 marks)
(iv) After how many seconds does it reach its farthest point? (2 marks)
(v) What is its acceleration? (2 marks)