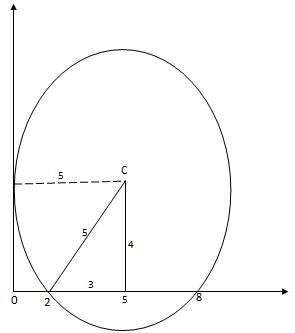Published on October 21st 2023 | 3 mins , 598 words
1. The length and width of a rectangle were measured as 12.4cm and 5.0cm respectively. Find to 4 significant figures, the percentage error in calculating the area of the rectangle (3mks)
Max Area =\(12.45\times5.05=62.875\)
Actual Area =\(12.5\times5.0=62.00\)
Min Area=\(12.35\times4.95=61.1325\)
Absolute Error = \(\frac{62.875-61.1325}{2}=0.87\)
%error = \(\frac{0.87}{62}\times100\)
\(= 1.403\%\)
Another approach is to calculate the total by summing the relative errors for each measurement and then multiplying the result by 100. So, the relative error in calculating the area is:
\(\frac{0.05}{12.4}+\frac{0.05}{5}\)
= 0.01403
Therefore, percentage error is:
= \( 0.01403 \times 100\)
=\(1.403 \%\)
2. The co-ordinates of a point A is (2,8,3) and B is (-4,-8,-5). A point P divides AB externally in the ratio 7:3. Determine the co-ordinates of P
So we have AP is 7 and PA is -3
Thus applying the ratio theorem, \(OP\) is given by:
\(\frac{7}{4}\left(\begin{array}{c}-4\\-8\\-5\end{array}\right) + \frac{-3}{4}\left(\begin{array}{c}2\\8\\3\end{array}\right) \)
= \(\left(\begin{array}{c} \small-7\\ \small-14\\ \small\frac{-34}{4} \end{array}\right) - \left(\begin{array}{c} \small\frac{3}{2} \\ \small-6\\ \small\frac{-9}{4} \end{array}\right) \)
= \( \left(\begin{array} {c}\small-8\frac{1}{2} \\ \small-20\\ \small-11 \end{array}\right) \)
Co-ordinates of P therefore is:
\(P(-8\frac{1}{2},-20, -11)\)
3. Solve for x:
\(( \log_{3}{x})^{2}-\frac{1}{2} \log_{3}{x} = \frac{3}{2}\)
The best way to solve for x in the above equation is by converting to a quadratic equation. Since \(\log_{3}{x}\) is common, we can subtitute it with \(t\).
Let \(\log_{3}{x} = t\)
Now when we plug in \(t\) we have:
\(( t)^{2}-\frac{1}{2}t = \frac{3}{2}\)
Multiplying through by 2 we have:
\(2t^{2}-t=3\)
We rearrange to make it in the form
\(ax^{2}+bx+c=0\)
\(2t^{2}-t-3=0\)
To solve by factorization method;
Product = \(-6t^{2}\)
sum = \(-t\)
Factors = (-3t,2t)
we rewrite the equation as:
\(2t^{2}-3t+2t-3=0\)
We group and factorize;
\(t(2t-3)+1(2t-3)=0\)
\((t+1)(2t-3)=0\)
either \(t+1)=0 or
\(2t-3)=0
t=-1 or t =1.5
But \(\log_{3}{x}=t \) therefore we need to replace with -1 and then with 1.5
Let's begin with -1;
\(\log_{3} {x}=-1 \)
This implies \(x=3^{-1}\)
\(x =\frac{1}{3}\)
Lastly, we substitute the other value of t
\(\log_{3} {x}=1.5 \)
So, \(x=3^{1.5}=5.196\)
4. A circle is tangent to the y-axis and intersects the x-axis at (2,0) and (8,0). Obtain the equation of the circle in the form \(x^{2}+y^{2}+ax+by+c=0\), where a, b and c are integers
To derive the equation of a circle, we utilize the geometric property that the bisector of any chord in a circle necessarily intersects the centre of the circle.
Additionally, it is established that a perpendicular line drawn at the point of tangency with the circle's circumference must traverse through the centre of the circle.
Thus, considering the midpoint of the two x-coordinates as 5, and recognizing that the distance from the point of tangency to the centre of the circle equals the distance from the origin to point 5, it can be deduced that the distance from point 2 to the centre is likewise 5, as both represent radii of the same circle.
Applying the Pythagorean theorem, the height of the triangle is determined to be 4. Notably, this height corresponds to the y-coordinate of the centre of the circle. Consequently, the co-ordinates of the circle's centre are identified as C(5, 4).
Utilizing the centre co-ordinates, we can proceed to establish the equation of the circle. It is recognized that the general equation of a circle is expressed as follows:
\((x-a)^{2}+ (y-b)^{2} =r^{2}\)
\((x-5)^{2}+ (y-4)^{2} =5^{2}\)
\(x^{2}-10x+25+y^{2}-8y+16=25\)
\( x^{2} + y^{2} -10x-8y+16=0\)